DFS深度优先搜索遍历
本文共 1888 字,大约阅读时间需要 6 分钟。
转载: 超简单详细
图的邻接表矩阵存储图,包含一位数组和指向节点的结构体,栈实现访问节点,递归实现dfs.
深度优先搜索(DFS, Depth First Search)是一个针对图和树的遍历算法。早在19世纪就被用于解决迷宫问题。
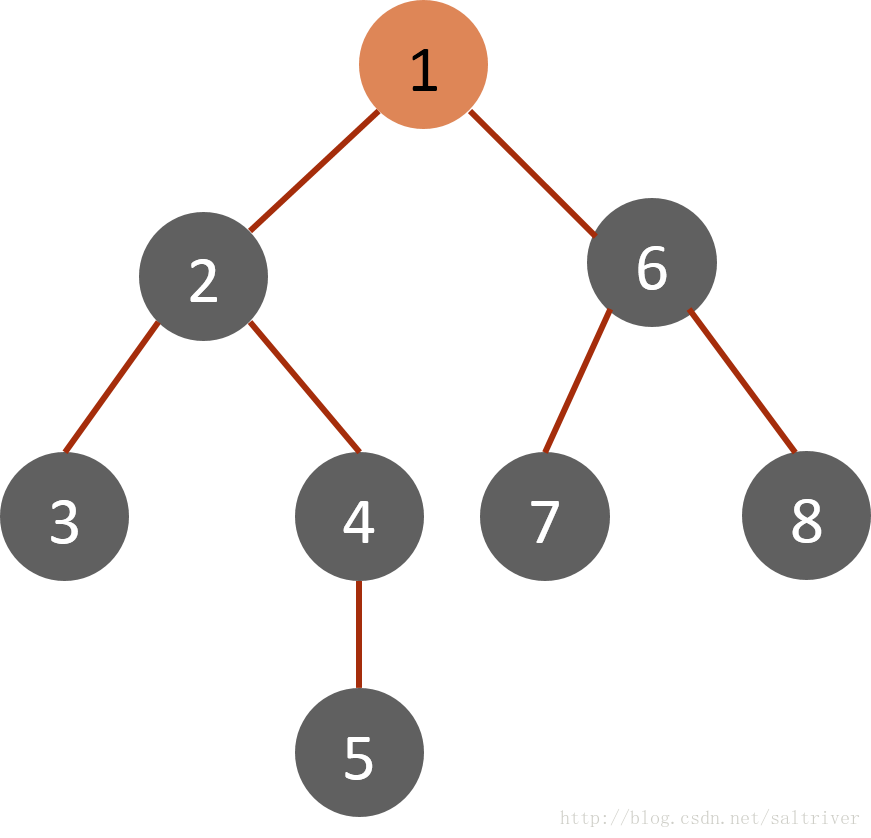
对于下面的树而言,DFS方法首先从根节点1开始,其搜索节点顺序是1,2,3,4,5,6,7,8(假定左分枝和右分枝中优先选择左分枝)。
 DFS的实现方式相比于BFS应该说大同小异,只是把queue换成了stack而已,stack具有后进先出LIFO(Last Input First Output)的特性,DFS的操作步骤如下: 1、把起始点放入stack; 2、重复下述3步骤,直到stack为空为止:
DFS的实现方式相比于BFS应该说大同小异,只是把queue换成了stack而已,stack具有后进先出LIFO(Last Input First Output)的特性,DFS的操作步骤如下: 1、把起始点放入stack; 2、重复下述3步骤,直到stack为空为止: - 从stack中访问栈顶的点;
- 找出与此点邻接的且尚未遍历的点,进行标记,然后全部放入stack中;
- 如果此点没有尚未遍历的邻接点,则将此点从stack中弹出。
下面结合一个图(graph)的实例,说明DFS的工作过程和原理:
(1)将起始节点1放入栈stack中,标记为已遍历。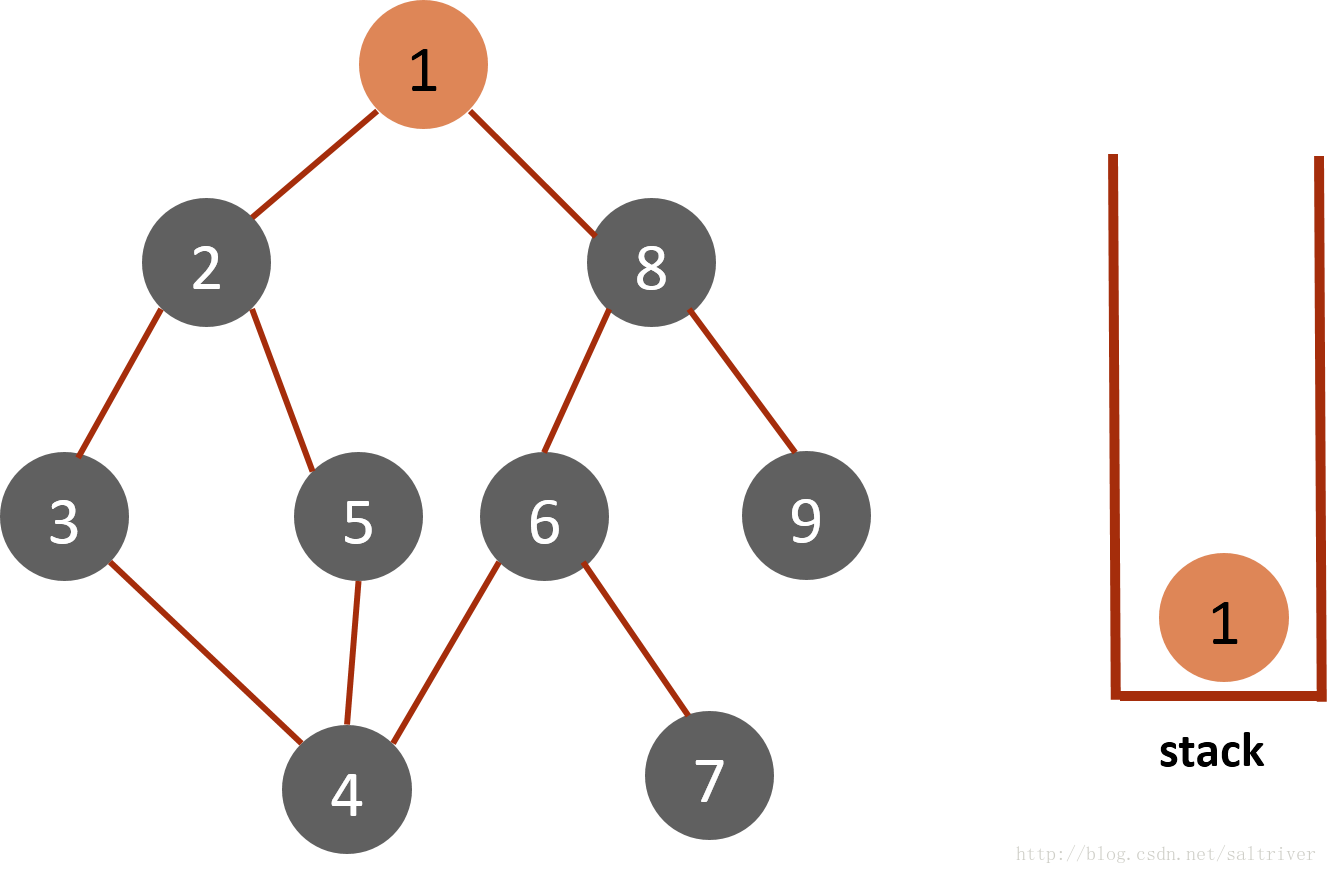 (2)从stack中访问栈顶的节点1,找出与节点1邻接的节点,有2,9两个节点,我们可以选择其中任何一个,选择规则可以人为设定,这里假设按照节点数字顺序由小到大选择,选中的是2,标记为已遍历,然后放入stack中。
(2)从stack中访问栈顶的节点1,找出与节点1邻接的节点,有2,9两个节点,我们可以选择其中任何一个,选择规则可以人为设定,这里假设按照节点数字顺序由小到大选择,选中的是2,标记为已遍历,然后放入stack中。 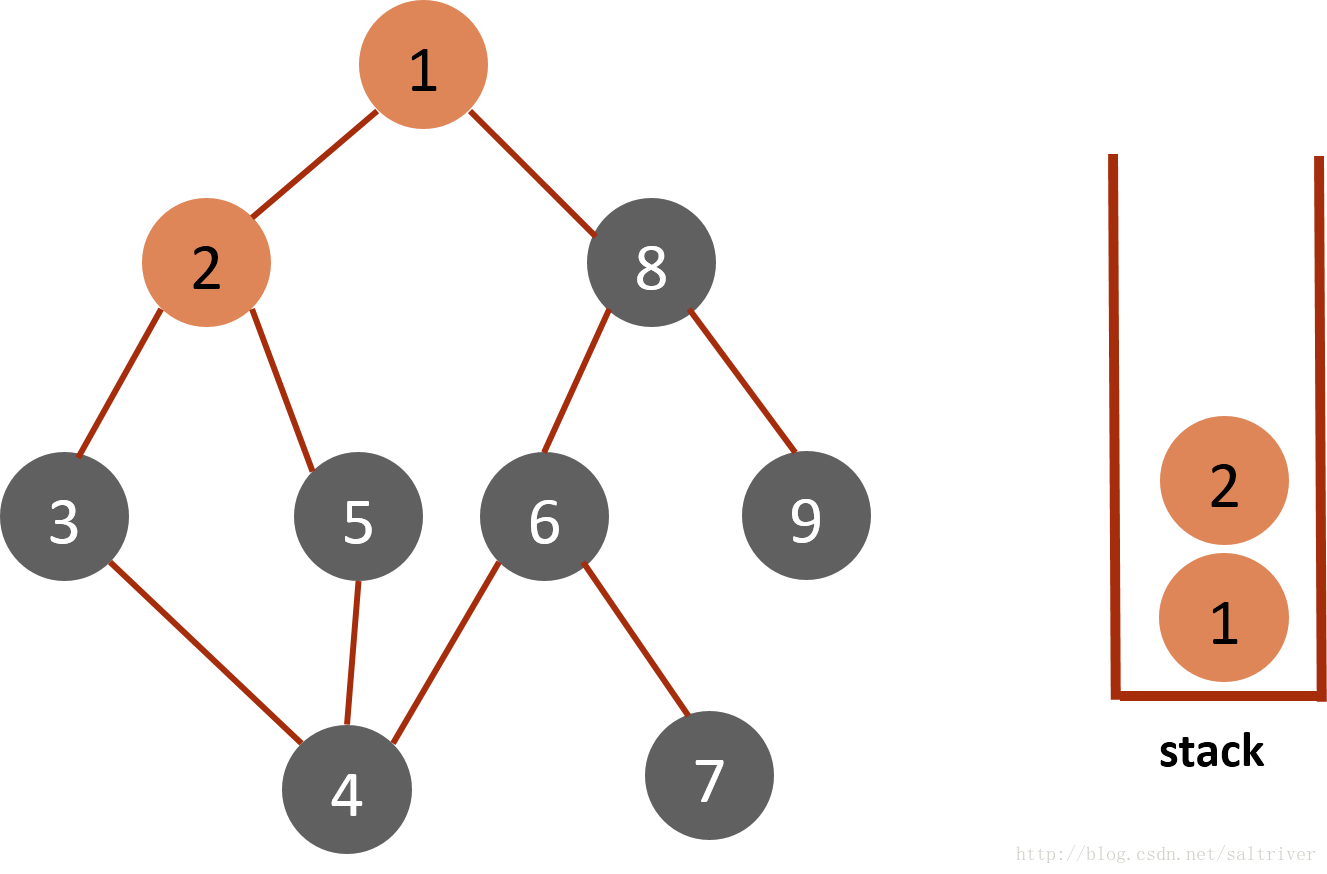 (3)从stack中取出栈顶的节点2,找出与节点2邻接的节点,有1,3,5三个节点,节点1已遍历过,排除;3,5中按照预定的规则选中的是3,标记为已遍历,然后放入stack中。
(3)从stack中取出栈顶的节点2,找出与节点2邻接的节点,有1,3,5三个节点,节点1已遍历过,排除;3,5中按照预定的规则选中的是3,标记为已遍历,然后放入stack中。 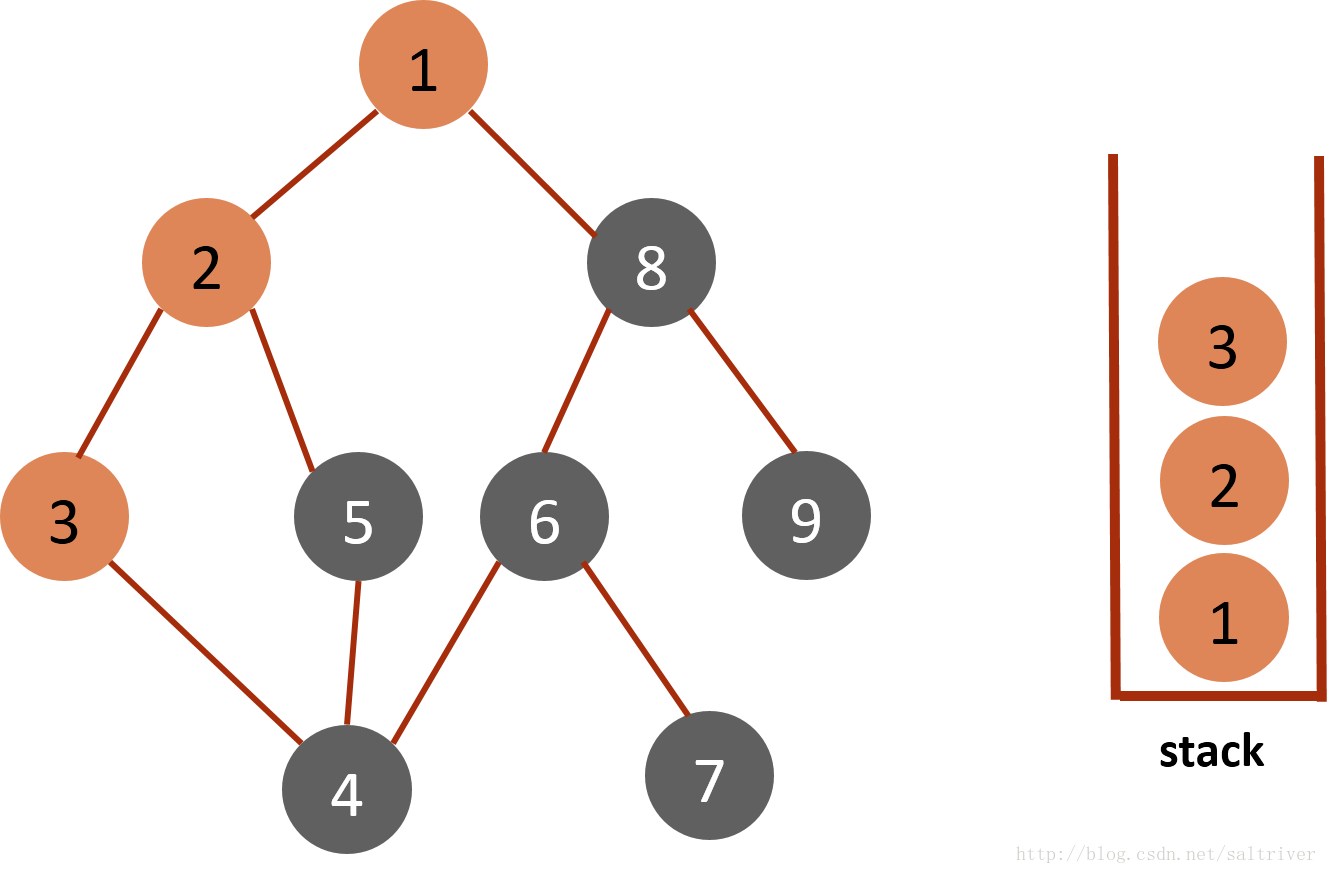 (4)从stack中取出栈顶的节点3,找出与节点3邻接的节点,有2,4两个节点,节点2已遍历过,排除;选中的是节点4,标记为已遍历,然后放入stack中。
(4)从stack中取出栈顶的节点3,找出与节点3邻接的节点,有2,4两个节点,节点2已遍历过,排除;选中的是节点4,标记为已遍历,然后放入stack中。 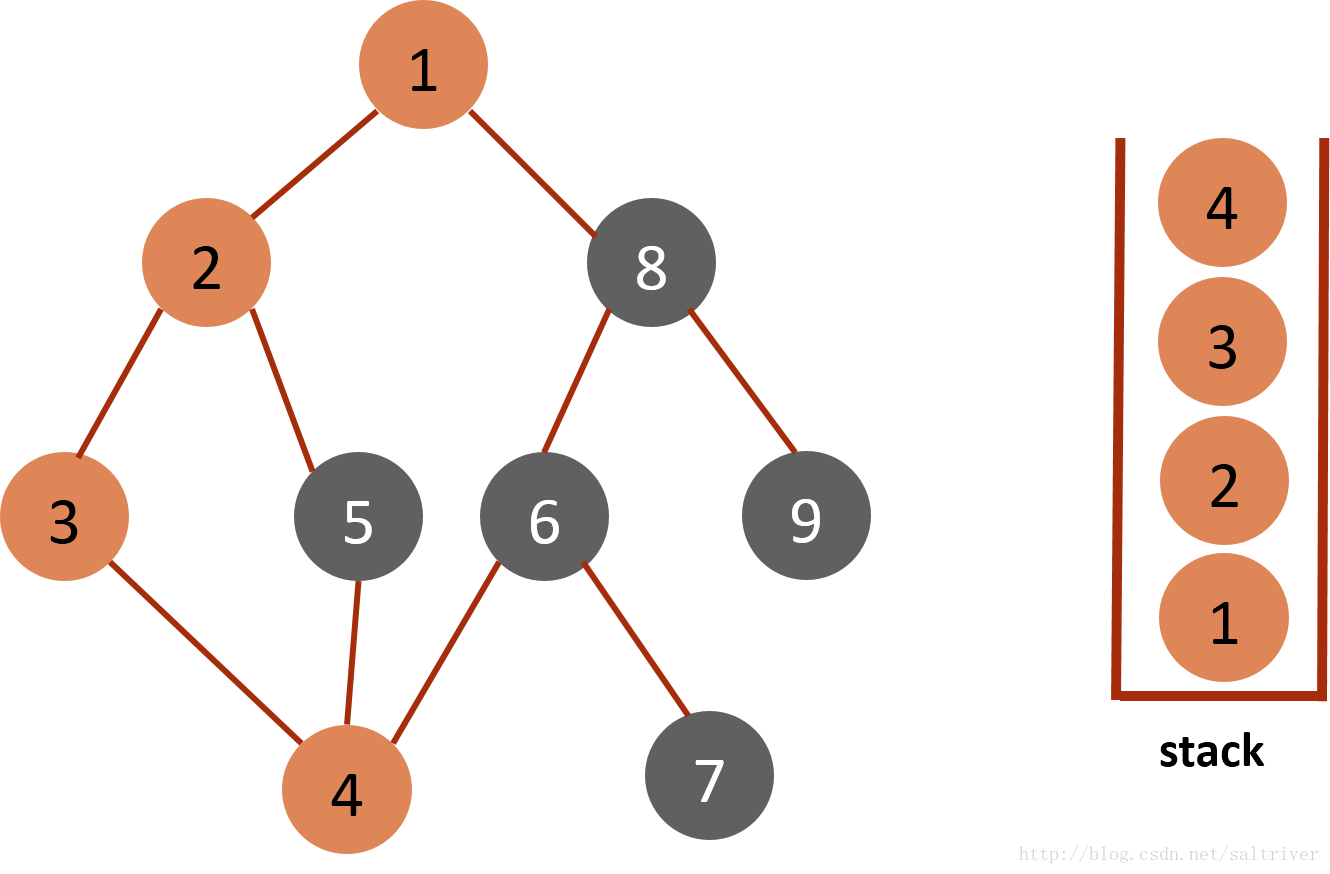 (5)从stack中取出栈顶的节点4,找出与节点4邻接的节点,有3,5,6三个节点,节点3已遍历过,排除;选中的是节点5,标记为已遍历,然后放入stack中。
(5)从stack中取出栈顶的节点4,找出与节点4邻接的节点,有3,5,6三个节点,节点3已遍历过,排除;选中的是节点5,标记为已遍历,然后放入stack中。 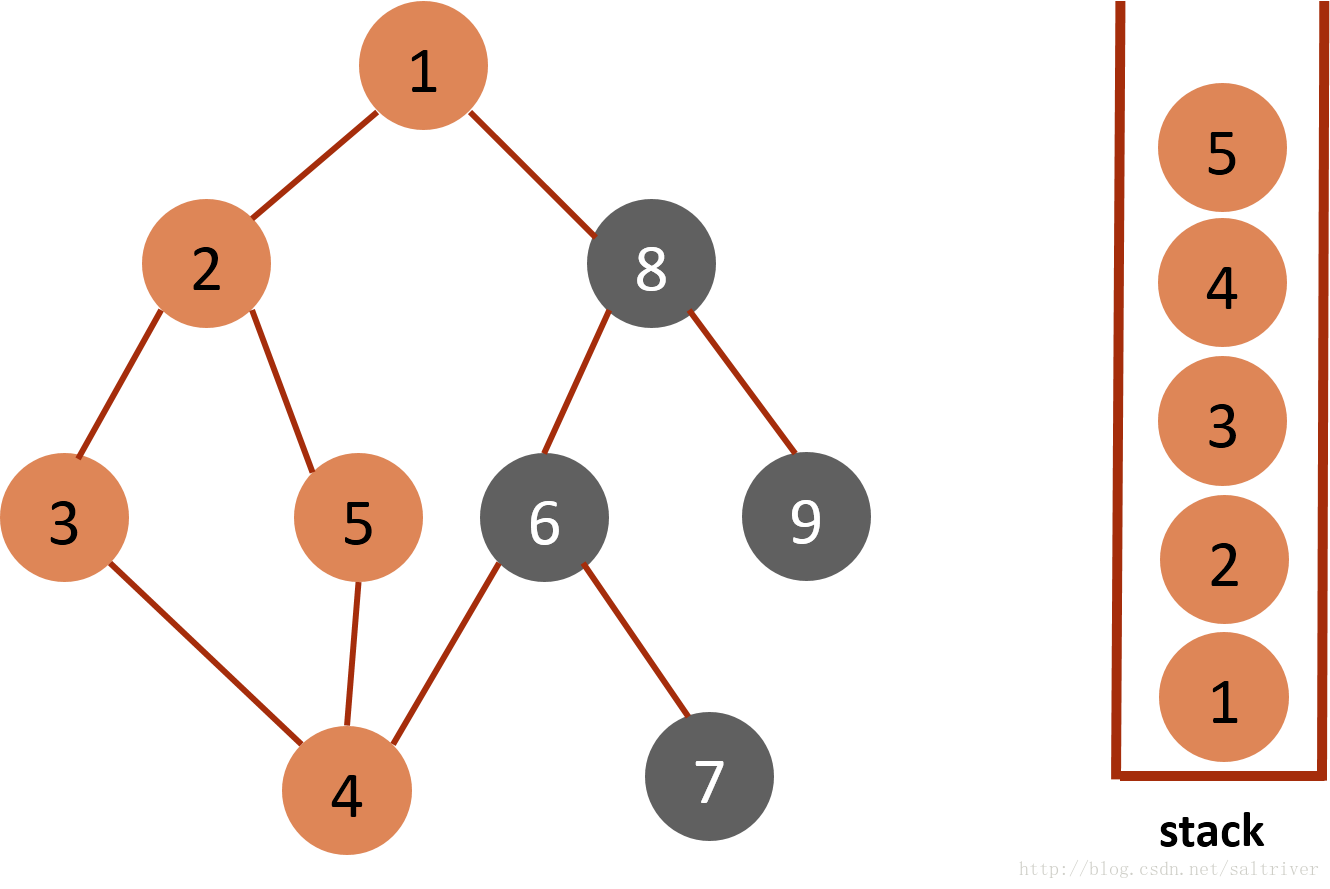 (6)从stack中取出栈顶的节点5,找出与节点5邻接的节点,有2,4两个节点,节点2,4都已遍历过,因此节点5没有尚未遍历的邻接点,则将此点从stack中弹出。
(6)从stack中取出栈顶的节点5,找出与节点5邻接的节点,有2,4两个节点,节点2,4都已遍历过,因此节点5没有尚未遍历的邻接点,则将此点从stack中弹出。 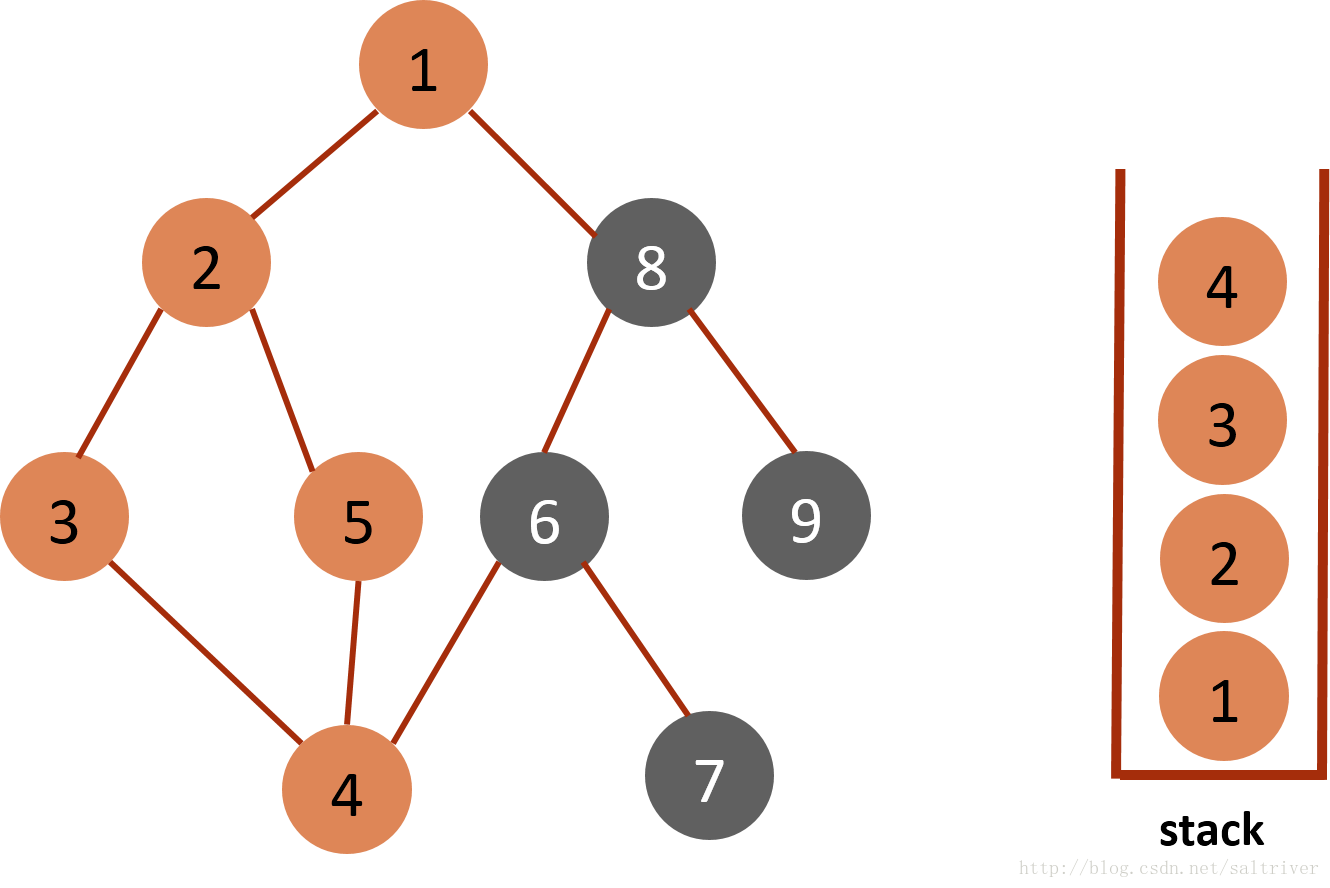 (7)当前stack栈顶的节点是4,找出与节点4邻接的节点,有3,5,6三个节点,节点3,5都已遍历过,排除;选中的是节点6,标记为已遍历,然后放入stack中。
(7)当前stack栈顶的节点是4,找出与节点4邻接的节点,有3,5,6三个节点,节点3,5都已遍历过,排除;选中的是节点6,标记为已遍历,然后放入stack中。 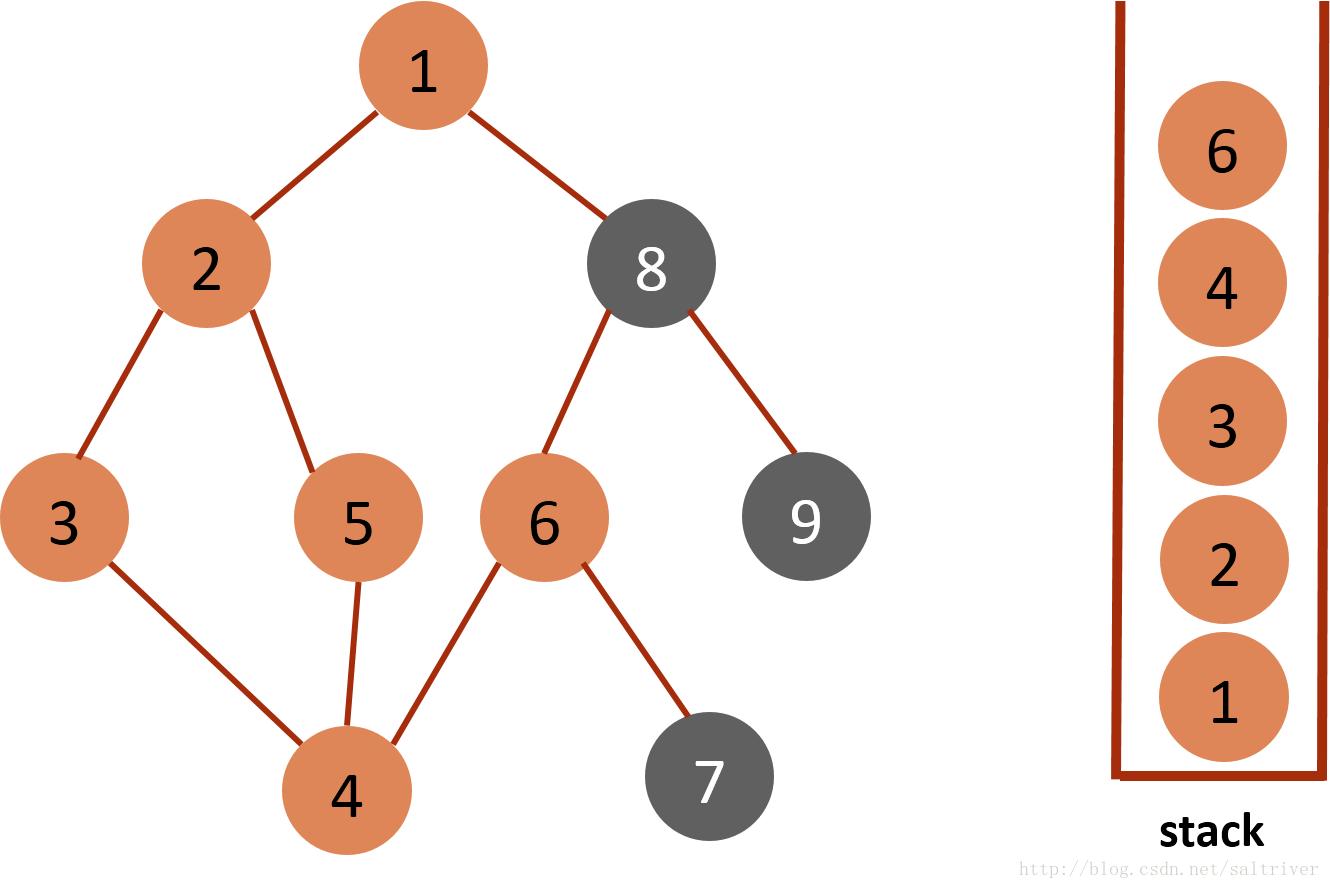 (8)当前stack栈顶的节点是6,找出与节点6邻接的节点,有4,7,8三个节点,4已遍历,按照规则选中的是7,标记为已遍历,然后放入stack中。
(8)当前stack栈顶的节点是6,找出与节点6邻接的节点,有4,7,8三个节点,4已遍历,按照规则选中的是7,标记为已遍历,然后放入stack中。 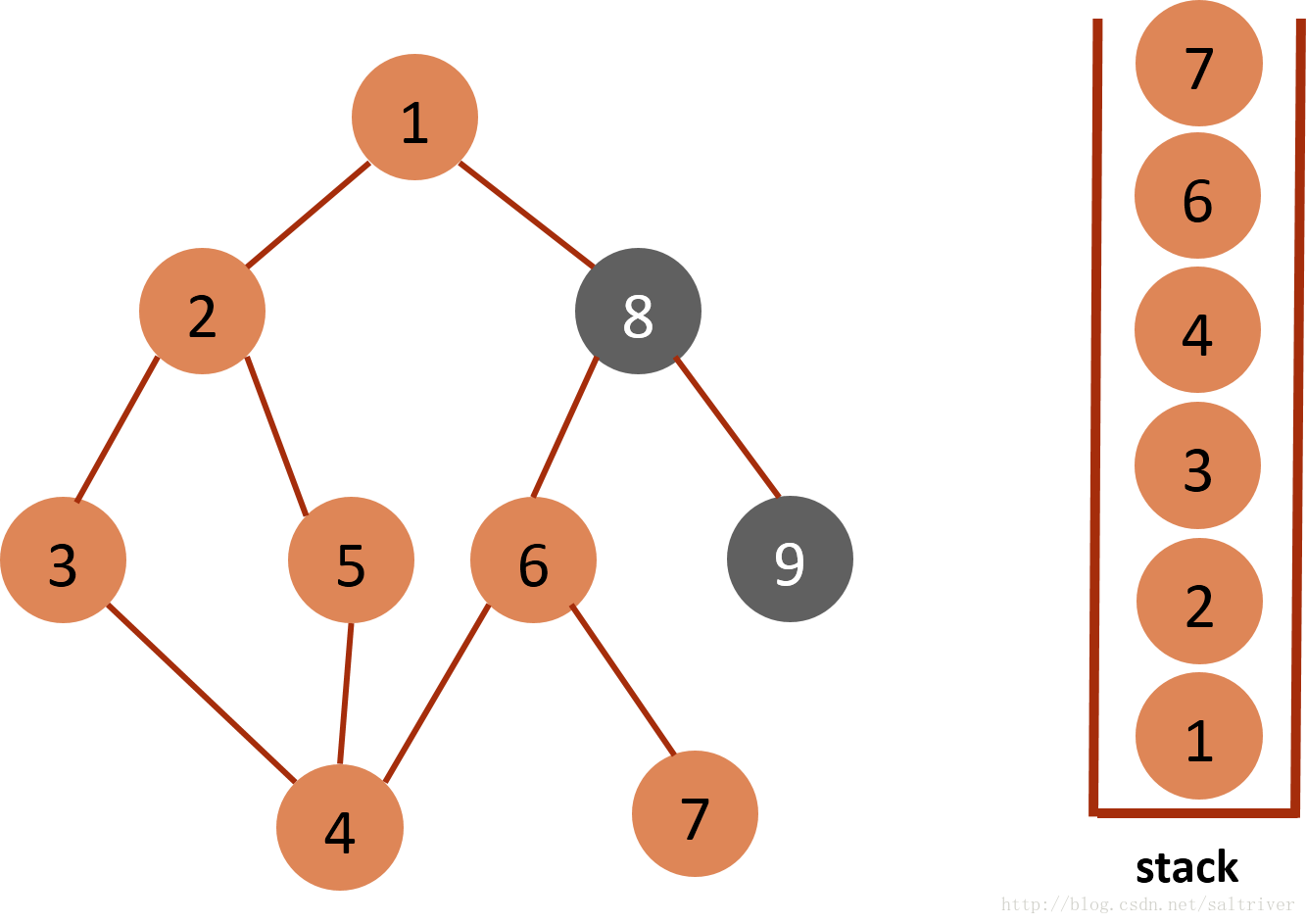 (9)当前stack栈顶的节点是7,找出与节点7邻接的节点,只有节点6,已遍历过,因此没有尚未遍历的邻接点,将节点7从stack中弹出。
(9)当前stack栈顶的节点是7,找出与节点7邻接的节点,只有节点6,已遍历过,因此没有尚未遍历的邻接点,将节点7从stack中弹出。 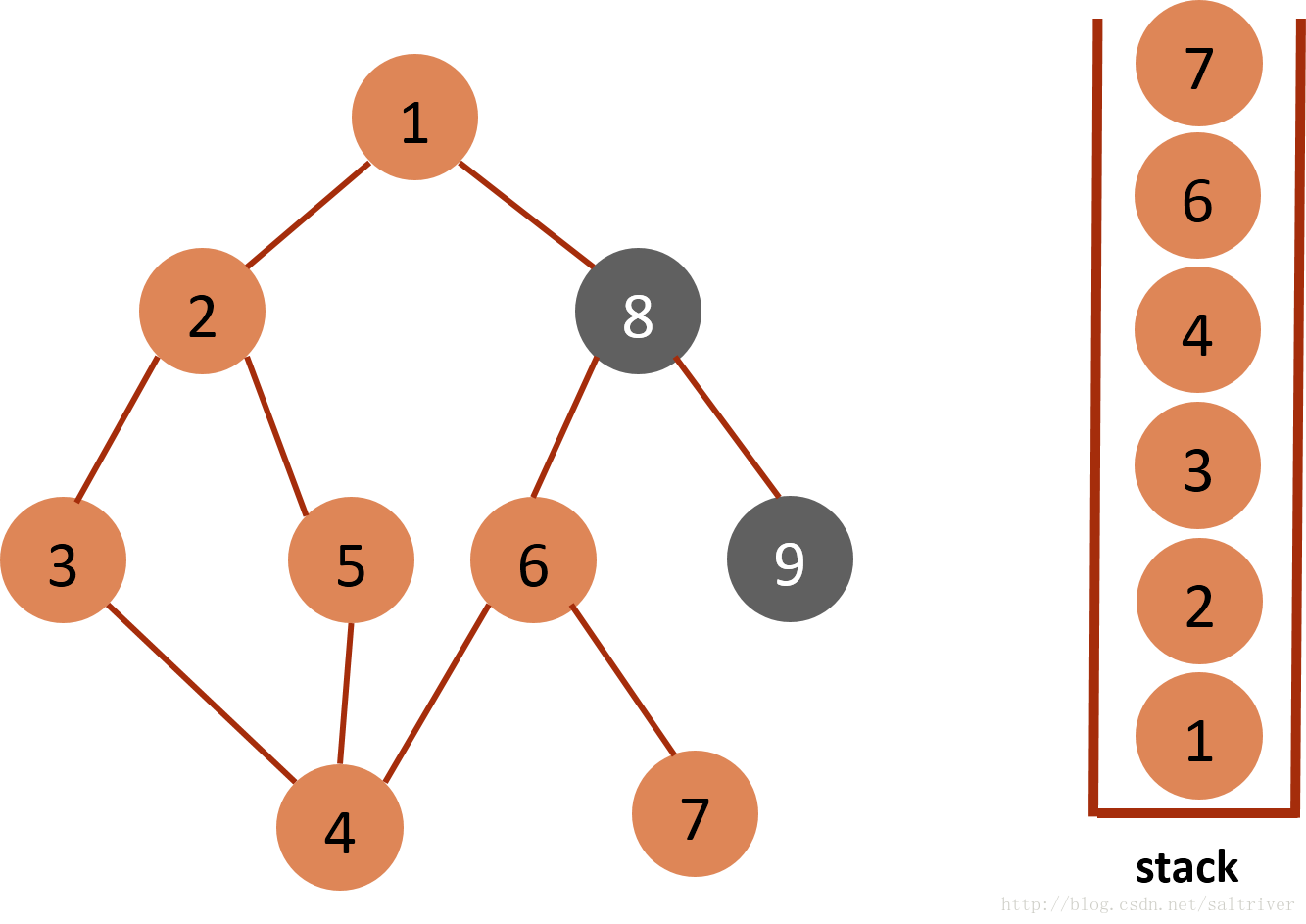 (10)当前stack栈顶的节点是6,找出与节点6邻接的节点,有节点7,8,7已遍历过,因此将节点8放入stack中。
(10)当前stack栈顶的节点是6,找出与节点6邻接的节点,有节点7,8,7已遍历过,因此将节点8放入stack中。 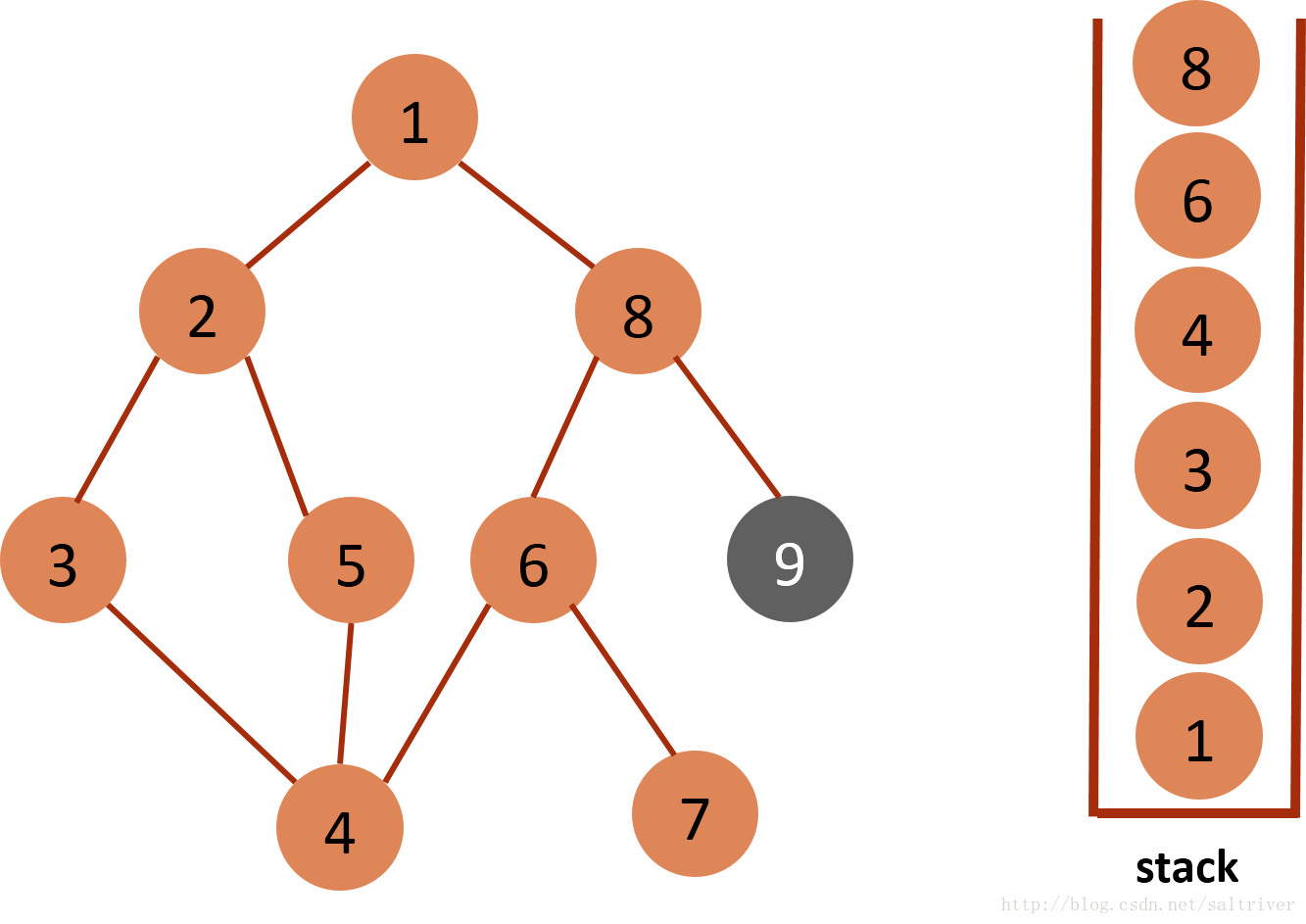 (11)当前stack栈顶的节点是8,找出与节点8邻接的节点,有节点1,6,9,1,6已遍历过,因此将节点9放入stack中。
(11)当前stack栈顶的节点是8,找出与节点8邻接的节点,有节点1,6,9,1,6已遍历过,因此将节点9放入stack中。 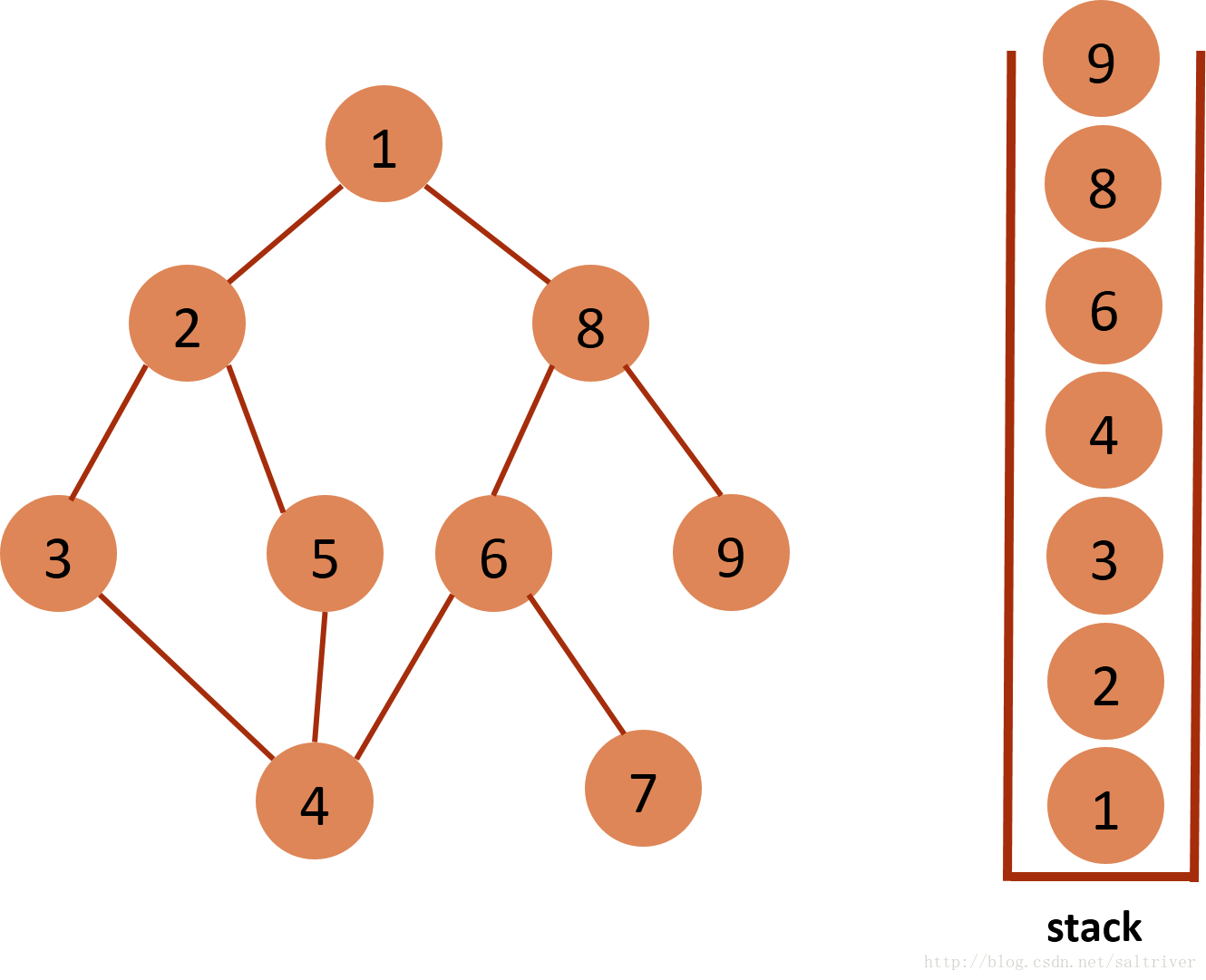 (12)当前stack栈顶的节点是9,没有尚未遍历的邻接点,将节点9弹出,依次类推,栈中剩余节点8,6,4,3,2,1都没有尚未遍历的邻接点,都将弹出,最后栈为空。 (13)DFS遍历完成。
(12)当前stack栈顶的节点是9,没有尚未遍历的邻接点,将节点9弹出,依次类推,栈中剩余节点8,6,4,3,2,1都没有尚未遍历的邻接点,都将弹出,最后栈为空。 (13)DFS遍历完成。 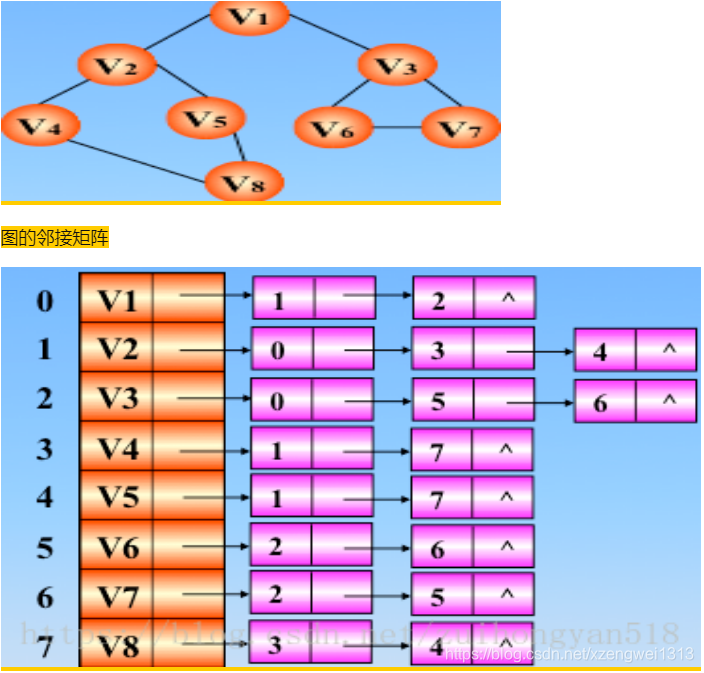
算法:
int visited[maxSize]; //访问标志的数组/* V是起点的编号,visited[]是一个全局的数组,作为顶点的访问标记,初始时所有的元素均为0,0表示被访问过,即所有的元素都没有被访问过。因图中可能存在回路,当前经过的顶点在将来还可能再次经过,所以要对每一个顶点进行标记,以免重复访问。 */void DFS(AGraph *G,int V){ ArcNode *p ; //图的顶点的搜索指针 visited[v]=1; //置已经访问 printf("%d",v); //输出访问过的顶点 visited(v); //函数visited()代表了一类访问顶点v的操作 p=G->adjlist[v].firstarc; //p指向顶点v的第一条边 while(p != null){ if(visited[p->adjvex]==0) //若顶点未访问,则递归访问它 DFS(G,p->adjvex); p = p->nextarc; //p指向顶点v的下一条边的终点 }}
你可能感兴趣的文章
MTTR、MTBF、MTTF的大白话理解
查看>>
mt_rand
查看>>
mysql -存储过程
查看>>
mysql /*! 50100 ... */ 条件编译
查看>>
mudbox卸载/完美解决安装失败/如何彻底卸载清除干净mudbox各种残留注册表和文件的方法...
查看>>
mysql 1264_关于mysql 出现 1264 Out of range value for column 错误的解决办法
查看>>
mysql 1593_Linux高可用(HA)之MySQL主从复制中出现1593错误码的低级错误
查看>>
mysql 5.6 修改端口_mysql5.6.24怎么修改端口号
查看>>
MySQL 8.0 恢复孤立文件每表ibd文件
查看>>
MySQL 8.0开始Group by不再排序
查看>>
mysql ansi nulls_SET ANSI_NULLS ON SET QUOTED_IDENTIFIER ON 什么意思
查看>>
multi swiper bug solution
查看>>
MySQL Binlog 日志监听与 Spring 集成实战
查看>>
MySQL binlog三种模式
查看>>
multi-angle cosine and sines
查看>>
Mysql Can't connect to MySQL server
查看>>
mysql case when 乱码_Mysql CASE WHEN 用法
查看>>
Multicast1
查看>>
mysql client library_MySQL数据库之zabbix3.x安装出现“configure: error: Not found mysqlclient library”的解决办法...
查看>>
MySQL Cluster 7.0.36 发布
查看>>